Pythonで三次元座標を扱うvol.2 〜可視化〜

今回は三次元座標を可視化するテクニックについて紹介していきます。

Pythonで可視化といえばmatplotlibが有名ですが、PythonらしくないAPI（当たり前）とあまりリッチなグラフを作れないという点が気に入らなかったので、今回はPlotlyを使ってみたいと思います。

環境

一応、筆者の環境を。

Python : 3.6.3
numpy : 1.13.3
plotly : 2.2.3

Python : 3.7.0, plotly : 3.4.1でも動作確認しました（2018/11/10）。

Plotlyについて

Plotlyとは？

Plotlyはインタラクティブなグラフを作成・共有するためのサービスです。表示にはWebGLを利用しているため、クロスプラットフォームかつ高速に動作するグラフが作成できます。

グラフ化ツール自体はオープンソースで開発されており、Python、MATLAB、R、JavaScript、Scalaなどの言語でAPIが無料で提供されています。また2018年1月現在、無料アカウントを作成すれば、オンライン上で25個のグラフを編集・保存・公開できるようです（ただしそれ以上のグラフを保存したり、グラフをprivateにしたい場合は有料のアカウントが必要になります）。

今回はオフラインで描画するだけなので、アカウントの作成は必要ありません。普通のPythonライブラリと同じように扱います。

インストール

PlotlyのPythonライブラリはpipからインストールできます。

python3 -m pip install plotly

インポート

普段どおりにモジュールをインポートします。

以降、サンプルコードを実行するときは、次のようにモジュールをインポートしておいてください。

import plotly.offline as po
import plotly.graph_objs as go
import numpy as np

# Jupyte Notebookに出力する場合は次のコマンドを実行しておく（後述）
plotly.offline.init_notebook_mode(connected=True)

出力方法

Plotlyのオフラインモードには2つの出力方法があります。

1つ目はhtmlファイルとして出力する方法です。これにはplotly.offline.plot()を使います。このコマンドを実行するとカレントディレクトリにhtmlファイルが保存されブラウザで表示されます。

2つ目はJupyter Notebook上に表示する方法です。これにはplotly.offline.iplot()を使います。このコマンドを実行するとnotebookの出力欄にグラフが表示されるようになります。

Jupyter Notebookを使う場合は、notebookのカーネルを起動した後に、次のコマンドを実行しておいてください。

plotly.offline.init_notebook_mode(connected=True)

以降のサンプルコードではplotly.offline.iplot()の方を使っていきます。

グラフ作成の流れ

Plotlyではまずプロットする点や線の情報を持ったtraceのリスト（data）とグラフのレイアウトの情報を持ったlayoutを作成します。そこからfigureを作り、プロットすることでグラフを作成します。

各オブジェクトの作成にはplotly.graph_objs内の関数を使いますが、traceもlayoutもfigureも実態は入れ子になったdictですので、簡単に中身を確認・編集できます。

またplotly.figure_factoryにはplotly.graph_objsをラップした、定型のグラフを描画するための関数が用意されています。よくあるグラフをサクッと描画したいときはこちらを使うほうがラクです。

その他の情報は公式リファレンスやgithubのソースコードを確認してください。

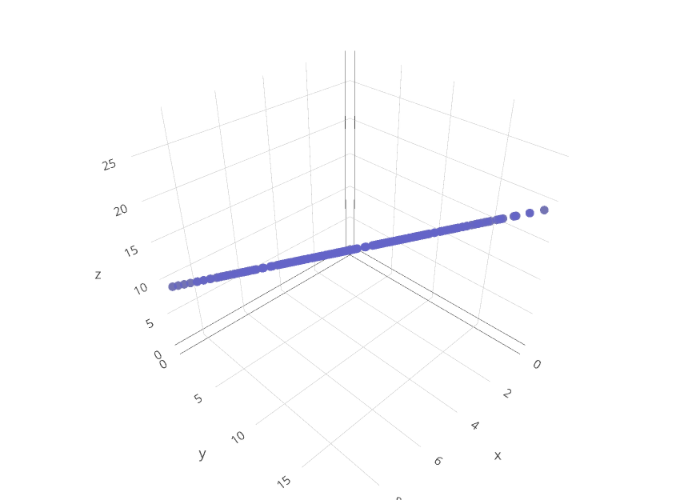
頂点のプロット

それでは手始めに頂点を描画してみます。

若干回りくどいですが前回の記事に合わせて、三次元座標をnumpy.ndarrayに整形し、それをプロットするという手順で書いてみます。

ソースコードの例

# 格子状に座標を生成
grid = np.mgrid[0:10, 0:20]
grid_x = grid[0].flatten()
grid_y = grid[1].flatten()
grid_z = grid_x + grid_y
points = np.array(list(zip(grid_x, grid_y, grid_z)))

# プロットのためにxyzごとのリストに分解
xs = points[:,0]
ys = points[:,1]
zs = points[:,2]

# traceを作成
trace = go.Scatter3d(
    x=xs,
    y=ys,
    z=zs,
    mode='markers',
    marker=dict(
        color='rgb(100,100,200)',
        size=5,
        opacity=0.8
    )
)
# layoutを作成
layout = go.Layout(
    # デフォルトでは描画領域が狭いのでmarginを0に
    margin=dict(
        l=0,
        r=0,
        b=0,
        t=0
    ),
    # xyz軸のスケールを統一
    scene=dict(aspectmode='cube'),
)
# traceとlayoutからfigureを作成
fig = go.Figure(data=[trace], layout=layout)
# プロット
po.iplot(fig, filename='sample-verts')

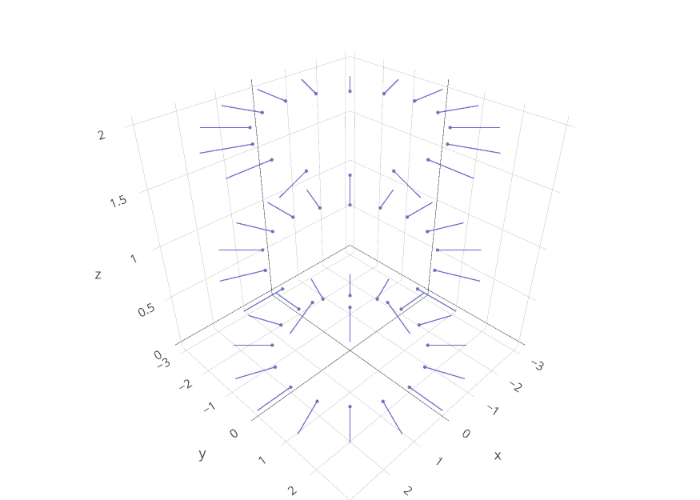
ベクトルのプロット

次にベクトルを描画してみます。

三次元上に矢印をプロットする機能はないようなので、線分を引いて根本にマーカーを置くことでベクトルを表現してみます。

ソースコードの例

# 円柱状に座標を生成
grid = np.mgrid[0:16, 0:3]
grid_ang = grid[0].flatten()
grid_z = grid[1].flatten()
grid_x = 2*np.cos(2*grid_ang*np.pi/16)
grid_y = 2*np.sin(2*grid_ang*np.pi/16)
points = np.array(list(zip(grid_x, grid_y, grid_z)))

# プロットのためにxyzごとにリストに分解
xs = points[:,0]
ys = points[:,1]
zs = points[:,2]

data = []
# マーカー
data.append(go.Scatter3d(
        x=xs,
        y=ys,
        z=zs,
        mode='markers',
        marker=dict(
            color='rgb(100,100,200)',
            size=2,
            opacity=0.8
        )
    ))
# 線分
for x, y, z in points:
    data.append(go.Scatter3d(
            x=[x, x+x/2],
            y=[y, y+y/2],
            z=[z, z],
            mode='lines',
            marker=dict(
                color='rgb(100,100,200)',
                size=5,
                opacity=0.8
            )
        ))
layout = go.Layout(
    margin=dict(
        l=0,
        r=0,
        b=0,
        t=0
    ),
    # xyz軸のスケールを統一
    scene=dict(aspectmode='cube'),
    showlegend=False,
)
fig = go.Figure(data=data, layout=layout)
po.iplot(fig, filename='sample-vecs')

平面のプロット

次は平面を描画してみます。 Plotlyには三次元の平面を描画するためのAPIがいくつかあります。

plotly.graph_objs.Surface()
- https://plot.ly/python/3d-surface-plots/
- 格子状の(x,y)座標と対応するzの値を入力として3Dグラフを描画する。
plotly.graph_objs.Mesh3d()
- https://plot.ly/python/3d-mesh/
- 三角ポリゴンから構成されるメッシュオブジェクトを描画する。
- 頂点座標のリスト、ポリゴンごとの頂点インデックスのリストを入力とする。
- 頂点座標だけ渡し、自動的にポリゴンを生成させることもできる（詳細はリファレンスのalphahullオプションの項を参照）。
- デフォルトではポリゴンの枠線が描画されない。
plotly.figure_factory.create_trisurf
- https://plot.ly/python/trisurf/
- Mesh3d()をラップしたもの。
- 頂点座標のリスト、ポリゴンごとの頂点インデックスのリストを入力とする。
- ポリゴンの自動配色と枠線の描画がおこなわれる。
- なぜかポリゴンを1つだけ描画しようとするとコケる。

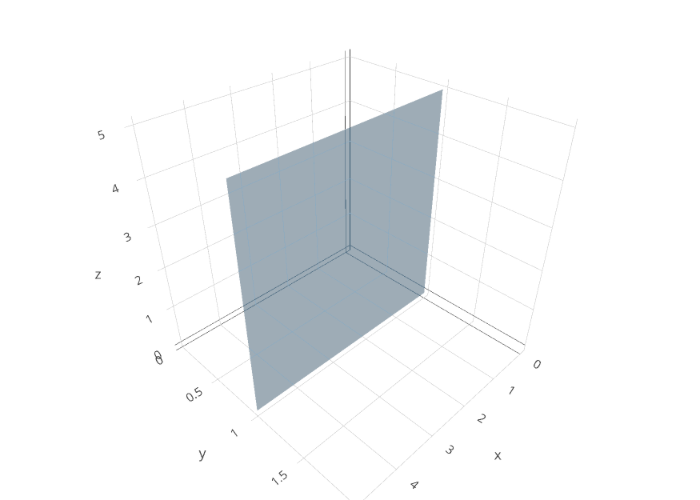
とりあえずここではplotly.graph_objs.Mesh3d()を使った例を紹介します。

(0,1,0),(5,1,0),(5,1,5),(0,1,5)を頂点とする四角形の平面を、0,1,2番目の頂点からなる三角ポリゴンと0,2,3番目の頂点からなる三角ポリゴンの2つに分けて描画しています。

ソースコードの例

※ go.Data(go.Mesh3d(...としていましたが、go.Dataが非推奨になったらしいのでリストに変更しました（2018/11/10）

data = [go.Mesh3d(
        x=[0, 5, 5, 0],
        y=[1, 1, 1, 1],
        z=[0, 0, 5, 5],
        i=[0, 0],
        j=[1, 2],
        k=[2, 3],
        opacity=0.4
    )]
layout = go.Layout(
    margin=dict(
        l=0,
        r=0,
        b=0,
        t=0
    ),
    # xyz軸のスケールを統一
    scene=dict(aspectmode='cube'),
)
fig = go.Figure(data=data, layout=layout)
po.iplot(fig, filename='sample-plane')

メッシュオブジェクトのプロット

最後にメッシュオブジェクトを描画してみます。

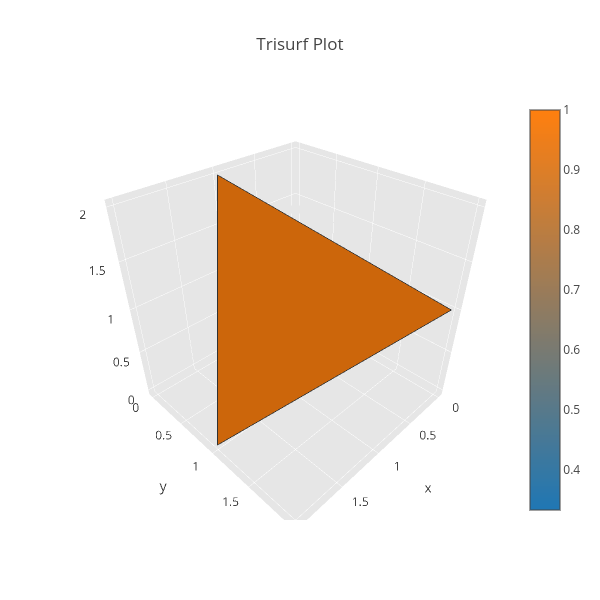
立体を描画するときは配色とポリゴンの枠線がないと形状がわかりにくくなってしまうので、ここではplotly.figure_factory.create_trisurfを使ってみます。

先ほどと同じように頂点座標とポリゴンごとの頂点インデックスのリストを入力としています。

ソースコードの例

import plotly.figure_factory as ff

fig = ff.create_trisurf(
        x=[0, 1, 2, 0],
        y=[0, 0, 1, 2],
        z=[0, 2, 0, 1],
        simplices=[[0, 1, 2],[0, 1, 3],[0, 2, 3],[1, 2, 3]])
po.iplot(fig, filename="sample-mesh")